LA FORMA DE LA TIERRA

Para determinar correctamente las coordenadas geográficas (latitud, longitud y altura) de un punto sobre la superficie terrestre es necesario precisar y conceptualizar la forma de la tierra. Así, a simple vista el planeta tierra posee una simetría esférica, esto es, la forma del planeta es posible equipararla, aproximadamente, a la forma geométrica de una esfera. Sin embargo, los movimientos de rotación y traslación por citar algunos, como bien es conocido, ejercen una influencia de modo tal que la tierra no posea una geometría perfectamente circular, es decir, existe una acumulación de masa sobre la zona del ecuador y un achatamiento en los polos, es por esto que el radio de la tierra en estas latitudes es un poco mayor comparativamente con el radio en los polos. En general, el radio de la tierra es de 6378 kilómetros y la diferencia entre radios del ecuador y los polos es aproximadamente 21.385 metros. El problema de la determinación de la forma de la tierra es uno de los más antiguos de la geodesia y se ha encontrado que puede ser resuelto desde dos puntos de vista: geométrico y otro dinámico o físico.

En este sentido, la tierra posee tres superficies: un Geoide, un Elipsoide y una superficie Topográfica. Un punto a consideración es que gran parte de la superficie del planeta está cubierto por agua (cerca del 70 por ciento) y ésta a su vez tiende a definir su superficie en dirección a la gravedad, por ende, la superficie del planeta puede ser descrita en términos del nivel medio del mar. Se define Geoide como la forma geométrica que busca hacer una representación verdadera de la tierra. En términos más rigurosos, el Geoide es definido como “Una superficie equipotencial de referencia hipotéticamente coincidente con el nivel medio del mar en calma. “[1] Ahora bien, el Geoide por ser una figura irregular (debido a que es una superficie de nivel del océano y la superficie terrestre) resulta casi imposible hacer algún tipo de medición, por tal motivo, se ha adoptado el elipsoide como figura geométrica necesaria para elaborar todo el tratamiento matemático respectivo. Un elipsoide (conocido también como esferoide) es “Un modelo fisicomatemático que representa a la Tierra, caracterizado por las constantes geométricas a (semieje mayor), b (semieje menor) y f (aplanamiento), y los parámetros físicos ω (velocidad angular de rotación) y m (masa)”[2], es por ello que emplear esta superficie es bastante apropiado para la definición de sistemas de coordenadas y en general sistemas de referencia espacial. Acudiendo a las definiciones geométricas del cálculo vectorial un elipsoide de revolución resulta de rotar completamente una elipse sobre su eje menor. Una superficie topográfica se define entonces como una superficie real observable “la topografía se representa por cadenas montañosas, valles y depresiones, es decir, corresponde a la superficie de las plataformas oceánicas y continentales, y es la realidad espacial en la tierra.

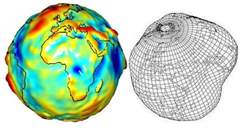
Figura 1. Representación del Geoide. Fuente: Tomado de http://www.cartografia.cl/beta/index.php/noticias/861-sistemas-de-referencia-y-coordenadas-arcgis-101

Otro aspecto importante a tratar es la existencia de un segundo tipo coordenadas que pueden estar referidas a un punto, denominadas planas o cartesianas (desarrolladas sobre un plano euclidiano). Este tipo de coordenadas son llevadas a cabo mediante unas operaciones matemáticas que permiten representar o proyectar la superficie curva del planeta sobre un plano, y convertir las coordenadas geográficas mencionadas en el inciso anterior en coordenadas planas de este tipo X e Y o si se prefiere Nortes y Estes. No obstante, este proceso conlleva distorsiones de la superficie original en 3 dimensiones al convertirse a una superficie plana de 2 dimensiones, se tienen: la Conforme (conserva el ángulo entre dos puntos medidos en la superficie de referencia y en el mapa), la Equivalente (mantiene áreas) y la Equidistante (mantiene distancias verdaderas) deformaciones por supuesto asociadas a las variantes topológicas (formas, áreas, distancias, perímetros. [3]

Figura 2. Proyección cilíndrica empleada en la zona del ecuador. Fuente:  http://geografiaparaelaula.blogspot.com/2014_05_01_archive.html

REFERENCIAS:

[1] Guia Metodológica para la obtención de Alturas utilizando el Sistema GPS (Bogotá D.C. Colombia: Instituto Geográfico Agistín Codazzi, (s. f.).

[2] Cardenas A. Fundamentos de Geodesia y Topografía para Hidrografía.

[3] Olaya, V., Fundamentos en Sistemas de Información Geográfica.